1. 大盗阿福
大盗阿福
题目
https://www.acwing.com/problem/content/1051/
阿福是一名经验丰富的大盗。趁着月黑风高,阿福打算今晚洗劫一条街上的店铺。
这条街上一共有 $N$ 家店铺,每家店中都有一些现金。
阿福事先调查得知,只有当他同时洗劫了两家相邻的店铺时,街上的报警系统才会启动,然后警察就会蜂拥而至。
作为一向谨慎作案的大盗,阿福不愿意冒着被警察追捕的风险行窃。
他想知道,在不惊动警察的情况下,他今晚最多可以得到多少现金?
输入格式
输入的第一行是一个整数 $T$,表示一共有 $T$ 组数据。
接下来的每组数据,第一行是一个整数 $N$ ,表示一共有 $N$ 家店铺。
第二行是 $N$ 个被空格分开的正整数,表示每一家店铺中的现金数量。
每家店铺中的现金数量均不超过1000。
输出格式
对于每组数据,输出一行。
该行包含一个整数,表示阿福在不惊动警察的情况下可以得到的现金数量。
数据范围
$1 \le T \le 50$,
$1 \le N \le 10^5$
输入样例:
1
2
3
4
5
2
3
1 8 2
4
10 7 6 14
输出样例:
1
2
8
24
样例解释
对于第一组样例,阿福选择第2家店铺行窃,获得的现金数量为8。
对于第二组样例,阿福选择第1和4家店铺行窃,获得的现金数量为10+14=24。
思路
常规线性DP
本题从线性DP的角度来思考相对来说比较简单,还是使用和前面一样的dp分析方法。
首先确定dp[i]代表的含义,本题中指的是前i个商店可以获取的总收益。
再来确定状态转移方程,对于第i个商店来说,能做的要么就是选,或者是不选。如果选的话,就不能选前一个;如果不选的话,其最大收益就是dp[i-1]。
所以状态转移方程为:
\[dp[i] = max(dp[i-1], dp[i-2] + w[i])\]状态机模型
状态机模型这里我理解更多的是给每一个dp[i]赋予一个状态维度,比如本题中,第i个商店有两个状态:抢劫或者是不抢劫。
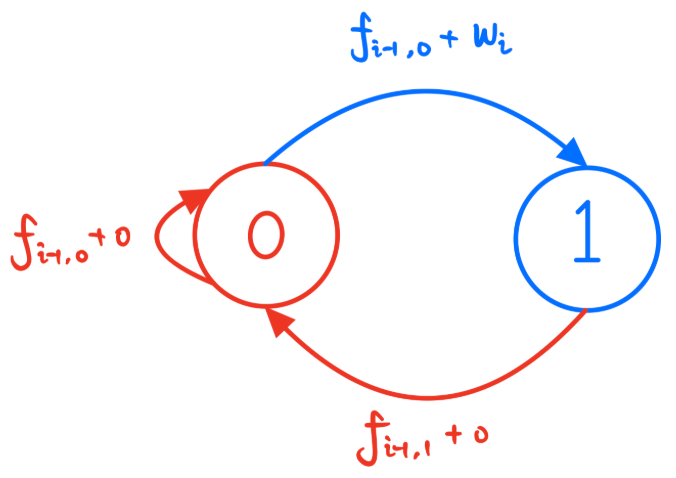
用状态机来表示状态的变化如下图所示:
其中,0代表未偷,1代表偷了。如果上一家没有偷,下一家就可以偷;上一家偷了,下一家只能不偷。不偷可以一直循环,但是偷了这一家,下一家的状态就一定要转化为不偷。
状态可以通过给dp[i]数组多加一个维度来表示,即dp[i][0]代表不偷,dp[i][1]代表偷。
如果要偷第i家店铺,则第i-1家店铺一定不能偷:
\(f[i][1] = f[i-1][0]\)
如果不偷第i家店铺,则第i-1家店铺可以偷,也可以不偷:
代码
常规线性DP
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <iostream>
#include <bitset>
#include <algorithm>
#include <queue>
using namespace std;
#define ll long long
#define rep(i, x, y) for(int i = x; i <= y; i ++)
#define pre(i, x, y) for(int i = x; i >= y; i --)
ll gcd(ll a, ll b){return b == 0 ? a : gcd(b, a % b);}
ll lcm(ll a, ll b){return a / gcd(a, b) * b;}
const int N = 1e5 + 10;
int t;
int n;
int num[N];
int dp[N];
ll solve()
{
ans = 0;
rep(i, 1, n) dp[i] = 0;
// dp[i]表示的是前i加商店能获取到的最大值
dp[1] = num[1];
rep(i, 2, n)
{
dp[i] = max(dp[i - 2] + num[i], dp[i-1]);
}
return dp[n];
}
int main(void)
{
ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
cin >> t;
while(t --)
{
cin >> n;
rep(i, 1, n) cin >> num[i];
cout << solve() << endl;
}
return 0;
}
状态机模型
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include <iostream>
#include <bitset>
#include <algorithm>
#include <queue>
using namespace std;
#define ll long long
#define rep(i, x, y) for(int i = x; i <= y; i ++)
#define pre(i, x, y) for(int i = x; i >= y; i --)
ll gcd(ll a, ll b){return b == 0 ? a : gcd(b, a % b);}
ll lcm(ll a, ll b){return a / gcd(a, b) * b;}
const int N = 1e5 + 10;
int t;
int n;
int num[N];
int dp[N][2];
int ans;
ll solve()
{
ans = 0;
dp[1][1] = num[1];
dp[1][0] = 0;
rep(i, 2, n)
{
dp[i][0] = max(dp[i-1][0], dp[i-1][1]);
dp[i][1] = dp[i-1][0] + num[i];
}
return max(dp[n][0], dp[n][1]);
}
int main(void)
{
ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
cin >> t;
while(t --)
{
cin >> n;
rep(i, 1, n) cin >> num[i];
cout << solve() << endl;
}
return 0;
}